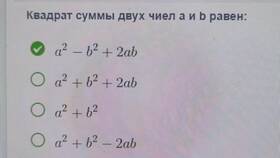Квадрат суммы - это математическое понятие, обозначающее результат возведения суммы двух или более чисел или алгебраических выражений во вторую степень. Данное понятие широко применяется в алгебре и математическом анализе.
Содержание
Формула квадрата суммы
Для двух слагаемых формула квадрата суммы выглядит следующим образом:
(a + b)² = a² + 2ab + b²
Геометрическая интерпретация
| Фигура | Пояснение |
| Квадрат со стороной (a+b) | Площадь такого квадрата равна (a+b)² |
| Разбиение квадрата | Состоит из квадратов a² и b², и двух прямоугольников ab |
Примеры применения
- Упрощение алгебраических выражений
- Решение квадратных уравнений
- Вычисления в физических задачах
- Статистические расчеты
Пример вычисления
Вычислим квадрат суммы чисел 4 и 3:
- (4 + 3)² = 7² = 49
- По формуле: 4² + 2×4×3 + 3² = 16 + 24 + 9 = 49
Квадрат суммы трех слагаемых
Формула для трех слагаемых:
(a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc
| Число слагаемых | Количество членов в разложении |
| 2 | 3 |
| 3 | 6 |
| n | n(n+1)/2 |
Доказательство формулы
- Запишем квадрат суммы как произведение: (a + b)² = (a + b)(a + b)
- Раскроем скобки: a×a + a×b + b×a + b×b
- Упростим выражение: a² + 2ab + b²
Применение в алгебре
- Разложение на множители
- Выделение полного квадрата
- Преобразование сложных выражений
- Доказательство тождеств
Ошибки при работе с квадратом суммы
| Распространенная ошибка | Правильное решение |
| (a + b)² = a² + b² | Пропущен член 2ab |
| (a - b)² = a² + b² | Должно быть a² - 2ab + b² |
Заключение
Квадрат суммы является важным алгебраическим понятием, которое находит широкое применение в различных разделах математики. Понимание и правильное применение соответствующей формулы позволяет существенно упрощать вычисления и преобразования математических выражений. Формула квадрата суммы входит в число основных алгебраических тождеств, которые необходимо знать для успешного решения математических задач.