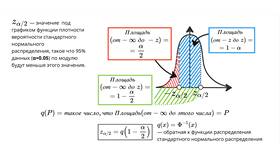
Доверительная вероятность определяет надежность статистических выводов и показывает вероятность того, что истинное значение параметра находится в пределах доверительного интервала. Рассмотрим методы ее расчета.
Содержание
Основные понятия
| Доверительная вероятность (P) | Вероятность, что доверительный интервал содержит истинное значение параметра |
| Уровень значимости (α) | Вероятность ошибки, α = 1 - P |
| Доверительный интервал | Диапазон значений, содержащий искомый параметр с заданной вероятностью |
Методы определения доверительной вероятности
Для нормального распределения
- Определите стандартную ошибку среднего (σ/√n)
- Выберите желаемый уровень доверия (90%, 95%, 99%)
- Найдите соответствующее значение z-критерия:
- 90% → z = 1.645
- 95% → z = 1.96
- 99% → z = 2.576
- Рассчитайте границы интервала: x̄ ± z*(σ/√n)
Для t-распределения (малые выборки)
| 1. Вычислите стандартную ошибку | s/√n, где s - выборочное стандартное отклонение |
| 2. Определите степени свободы | df = n - 1 |
| 3. Найдите t-значение | По таблице t-распределения для выбранного P и df |
Формулы расчета
| Для среднего значения | x̄ ± tα/2(s/√n) |
| Для доли | p̂ ± zα/2√(p̂(1-p̂)/n) |
| Для разности средних | (x̄1-x̄2) ± tα/2√(s12/n1 + s22/n2) |
Выбор уровня доверия
- 90% - для предварительных исследований
- 95% - стандартный уровень в научных работах
- 99% - для ответственных исследований
Практические примеры
Пример 1: Расчет для среднего
- Дано: n=100, x̄=50, σ=10, P=95%
- Стандартная ошибка: 10/√100 = 1
- z-значение: 1.96
- Доверительный интервал: 50 ± 1.96*1 → [48.04, 51.96]
Пример 2: Малые выборки
| Дано | n=25, x̄=80, s=15, P=90% |
| Степени свободы | 24 |
| t-значение | 1.711 |
| Интервал | 80 ± 1.711*(15/5) → [74.867, 85.133] |
Программные средства
- Excel: функции CONFIDENCE.NORM, CONFIDENCE.T
- R: qnorm(), qt()
- Python: scipy.stats.norm.ppf, scipy.stats.t.ppf
- Калькуляторы статистики онлайн
При выборе доверительной вероятности учитывайте компромисс между точностью и шириной интервала: чем выше доверие, тем шире интервал.