Сумма катетов прямоугольного треугольника является важной величиной при решении геометрических задач. Рассмотрим основные методы ее вычисления.
Содержание
Основные понятия
В прямоугольном треугольнике:
- Катеты - две стороны, образующие прямой угол
- Гипотенуза - сторона, противолежащая прямому углу
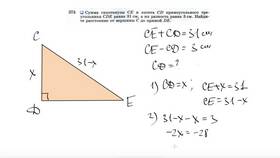
- Сумма катетов = a + b, где a и b - длины катетов
Способы нахождения суммы катетов
| Известные данные | Формула |
| Длины обоих катетов | a + b |
| Гипотенуза и один катет | a + √(c² - a²) |
| Площадь и один катет | a + (2S)/a |
| Острый угол и один катет | a + a·tan(α) или a + a/tan(α) |
Пошаговые методы вычисления
По известным катетам
- Измерьте длину первого катета (a)
- Измерьте длину второго катета (b)
- Сложите полученные значения: a + b
Через гипотенузу и катет
- Измерьте известный катет (a) и гипотенузу (c)
- Найдите второй катет по формуле: b = √(c² - a²)
- Сложите оба катета: a + b
Через площадь и катет
- Определите площадь треугольника (S) и один катет (a)
- Вычислите второй катет: b = (2S)/a
- Сложите значения катетов
Примеры расчетов
| Дано | Решение | Сумма катетов |
| a = 3, b = 4 | 3 + 4 | 7 |
| a = 5, c = 13 | b = √(169-25) = 12; 5 + 12 | 17 |
| S = 24, a = 6 | b = 48/6 = 8; 6 + 8 | 14 |
Практическое применение
- Расчет периметра прямоугольного треугольника
- Определение суммарной длины сторон в строительстве
- Решение задач на оптимизацию
- Геометрические построения
Ограничения и особенности
- Метод работает только для прямоугольных треугольников
- При использовании теоремы Пифагора убедитесь в правильности определения гипотенузы
- Все измерения должны быть в одинаковых единицах
- Для точных расчетов используйте калькулятор
Умение находить сумму катетов является базовым навыком в геометрии и применяется во многих практических задачах.