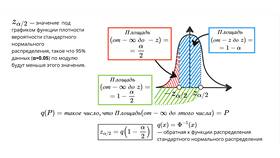
Доверительный интервал представляет собой диапазон значений, который с определенной вероятностью содержит истинное значение оцениваемого параметра. Рассмотрим методы расчета и интерпретации доверительных интервалов для различных типов данных.
Содержание
Основные понятия
- Доверительная вероятность (обычно 90%, 95% или 99%)
- Точечная оценка параметра
- Стандартная ошибка измерения
- Распределение выборки
Методы расчета доверительных интервалов
| Тип данных | Формула | Примечания |
| Среднее значение (норм. распределение) | x̄ ± z*(σ/√n) | z - критическое значение, σ - стандартное отклонение |
| Доля (биномиальное распределение) | p̂ ± z*√(p̂(1-p̂)/n) | p̂ - выборочная доля |
| Малые выборки (t-распределение) | x̄ ± t*(s/√n) | t - коэффициент Стьюдента |
Пошаговый алгоритм расчета
Определение параметров
- Выберите доверительный уровень (обычно 95%)
- Рассчитайте точечную оценку параметра
- Определите стандартную ошибку
- Найдите критическое значение распределения
Вычисление интервала
- Для среднего: используйте z- или t-статистику
- Для пропорций: применяйте нормальную аппроксимацию
- Для разности средних: учитывайте зависимость выборок
- Для регрессионных коэффициентов: используйте стандартные ошибки
Факторы, влияющие на ширину интервала
- Объем выборки (n) - обратная зависимость
- Доверительная вероятность - прямая зависимость
- Разброс данных - прямая зависимость
- Тип распределения - определяет формулу расчета
Практические рекомендации
- Для малых выборок используйте t-распределение
- При анализе пропорций проверьте условия np>5 и n(1-p)>5
- Для непараметрических данных применяйте бутстреп-методы
- Всегда указывайте доверительный уровень при отчете
Интерпретация результатов
Доверительный интервал 95% означает, что при многократном повторении исследования в 95% случаев вычисленный интервал будет содержать истинное значение параметра. Это не вероятность того, что параметр находится в данном конкретном интервале.