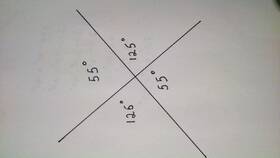
Теорема о сумме углов треугольника утверждает, что сумма внутренних углов любого плоского треугольника равна 180 градусам (или π радиан).
Содержание
Формулировка теоремы
Математическая запись
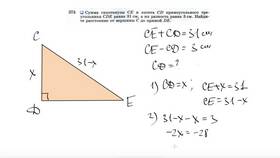
Для треугольника ABC с углами ∠A, ∠B и ∠C теорема записывается как:
∠A + ∠B + ∠C = 180°
Доказательство теоремы
Классическое доказательство
- Проведем через вершину C прямую, параллельную стороне AB
- Образовавшиеся углы при точке C будут равны углам A и B
- Сумма углов на прямой равна 180°
- Следовательно, ∠A + ∠B + ∠C = 180°
Примеры вычислений
| Тип треугольника | Угол A | Угол B | Угол C | Сумма |
| Равносторонний | 60° | 60° | 60° | 180° |
| Прямоугольный | 90° | 30° | 60° | 180° |
| Произвольный | 45° | 65° | 70° | 180° |
Следствия из теоремы
- В треугольнике не может быть более одного прямого или тупого угла
- Сумма острых углов прямоугольного треугольника равна 90°
- Внешний угол треугольника равен сумме двух внутренних, не смежных с ним
Исключения и обобщения
Невозможные случаи
Не существует треугольника с суммой углов:
- Меньше 180° в евклидовой геометрии
- Больше 180° в стандартной геометрии
Неевклидова геометрия
В других геометрических системах сумма углов треугольника может отличаться:
- В сферической геометрии сумма > 180°
- В геометрии Лобачевского сумма < 180°
Практическое применение
Решение задач
Теорема используется для:
- Нахождения неизвестных углов треугольника
- Доказательства равенства треугольников
- Построения геометрических фигур
Важность теоремы
Эта фундаментальная теорема лежит в основе многих разделов геометрии и находит применение в архитектуре, инженерии и компьютерной графике.